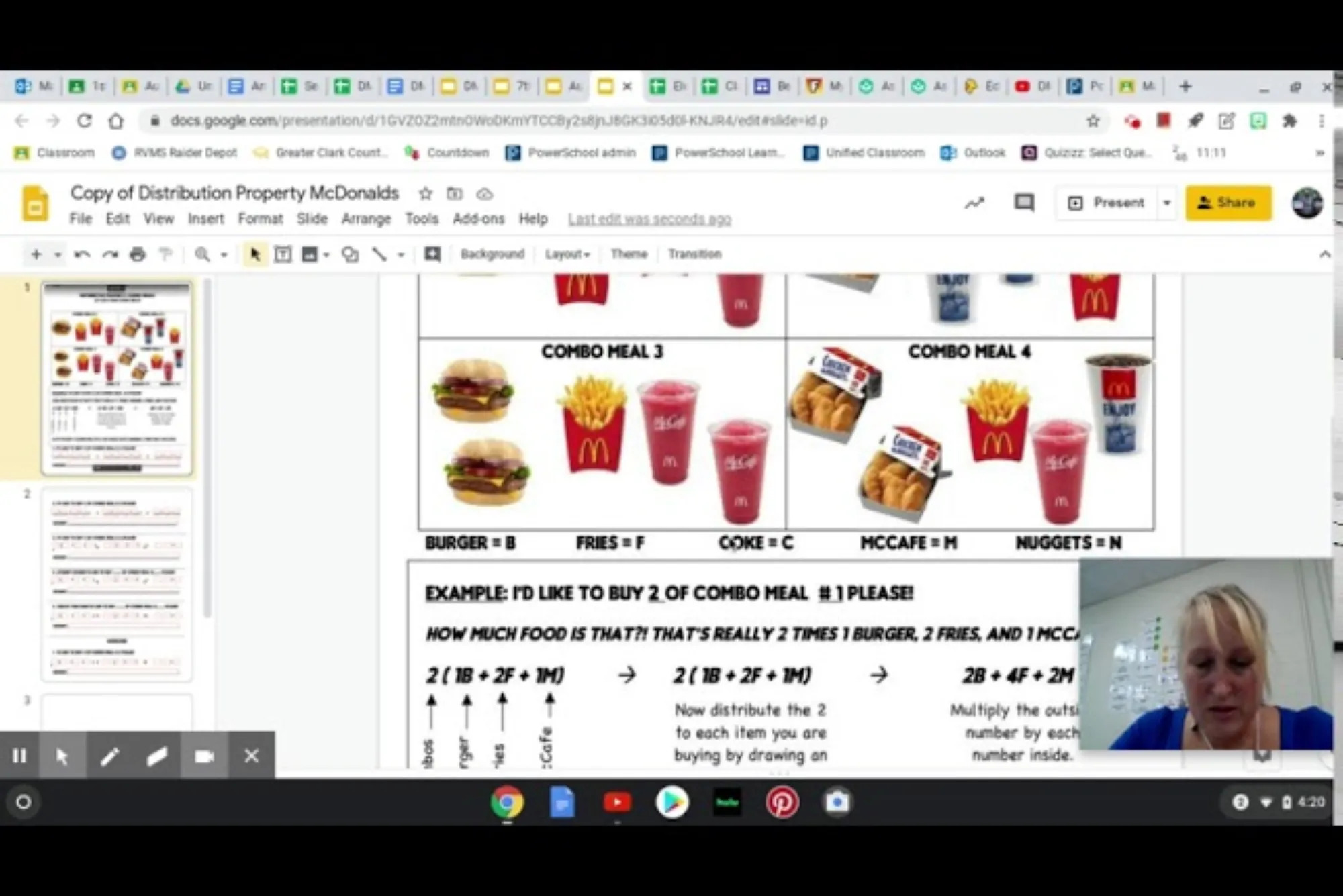
Mathematics often seems abstract, but applying concepts to real-world scenarios can make them more understandable. One of the most effective ways to comprehend the distributive property is by connecting it to something we can all relate to—ordering fast food. This allows us to break down the distributive property in a more engaging and tangible way.
The distributive property is an essential concept in mathematics, particularly when working with multiplication. It allows you to multiply a number by a sum or difference in a simpler way. Instead of multiplying the number by the whole sum at once, the distributive property lets you distribute the multiplication across the individual terms within the parentheses. This property is often represented in the form:
a(b + c) = ab + ac
In other words, if you have a number multiplying a sum inside parentheses, you can multiply that number by each term inside the parentheses separately, and then add the results.
To better understand the distributive property, let’s relate it to ordering fast food. Imagine you are at a fast food restaurant and you decide to buy several meals, each costing a certain amount. By applying the distributive property, you can calculate the total cost in a more manageable way.
For instance, suppose each meal costs $5, and you decide to order 3 meals. You could simply multiply 3 by 5, and you’d get the total cost:
3 * 5 = 15

However, using the distributive property can help break this problem into smaller pieces. You could think of it as multiplying 3 by a sum. For example:
3 * (2 + 3)
= (3 * 2) + (3 * 3)
= 6 + 9
= 15
As you can see, you get the same result, but by distributing the multiplication over the sum, you break the calculation into smaller, simpler steps. This method can be helpful in more complex situations as well.
Now imagine a scenario where you are ordering fast food for a group of friends. The cost of each meal is $8.50, and you need to order 5 meals. Using the distributive property, you can break this into two parts to make the calculation easier:
5 * 8.50 = 5 * (8 + 0.50)
= (5 * 8) + (5 * 0.50)
= 40 + 2.50
= 42.50
By applying the distributive property, we simplify the multiplication process, making it easier to perform the calculation mentally.
This approach becomes even more useful when dealing with larger numbers or more complex problems. Suppose you’re ordering a larger quantity of meals, say 7 meals at $10 each. Using the distributive property, you can break this down as follows:
7 * 10 = 7 * (5 + 5)
= (7 * 5) + (7 * 5)
= 35 + 35
= 70
This breakdown helps you avoid doing all the multiplication at once and simplifies the process of getting the total cost. By distributing the multiplication across smaller sums, you can tackle complex problems with greater ease.
At this point, you may wonder how to apply this concept to even larger or more complicated numbers. Let’s take another example: ordering 12 meals at $13.50 each. Using the distributive property, you can break it down into smaller calculations:
12 * 13.50 = 12 * (13 + 0.50)
= (12 * 13) + (12 * 0.50)
= 156 + 6
= 162
As you can see, breaking the multiplication into parts using the distributive property makes it easier to handle and reduces the complexity of larger numbers.
The distributive property is a powerful tool not only for simplifying calculations but also for gaining a deeper understanding of how multiplication works. By relating it to real-life scenarios, such as fast food ordering, it becomes easier to see the practical applications of this mathematical concept.
One helpful way to practice the distributive property is through interactive tools like Quizlet. Quizlet is a platform that allows students to create and study custom flashcards and quizzes. In the case of learning the distributive property, you could create a Quizlet set using real-life examples, such as fast food orders, to practice distributing multiplication over sums. This interactive approach reinforces the concept and allows students to see how the distributive property works in various contexts.
A Quizlet set focused on the distributive property with fast food examples could look something like this:
| Fast Food Orders | Multiplication Problem | Using the Distributive Property | Answer |
|---|---|---|---|
| 4 Meals at $6 each | 4 * 6 | 4 * (3 + 3) = (4 * 3) + (4 * 3) | $24 |
| 5 Meals at $8.50 each | 5 * 8.50 | 5 * (8 + 0.50) = (5 * 8) + (5 * 0.50) | $42.50 |
| 6 Meals at $7.25 each | 6 * 7.25 | 6 * (7 + 0.25) = (6 * 7) + (6 * 0.25) | $43.50 |
By practicing with these examples, you can better understand how the distributive property works and how to use it in real-life situations. Quizlet’s interactive quizzes and flashcards help reinforce this knowledge and provide immediate feedback, making learning more engaging and effective.
Using the distributive property also has applications in other areas of mathematics and real-world situations, beyond just fast food orders. For example, you can use the distributive property to solve problems involving time, distance, or even money management. It’s a versatile tool that simplifies complex calculations and makes them more manageable.
The beauty of the distributive property lies in its simplicity. While it may initially seem complicated, once you understand how it breaks down multiplication problems into smaller parts, it becomes a powerful tool for tackling more complex arithmetic. By using relatable examples, like fast food ordering, and interactive learning tools like Quizlet, you can master this concept and apply it to a wide range of problems.
In conclusion, the distributive property is an important concept in mathematics that allows us to simplify multiplication problems by distributing the multiplication across smaller parts. Using real-world examples, such as fast food orders, makes the concept more accessible and easier to understand. Tools like Quizlet can further enhance learning by providing interactive practice problems. By mastering the distributive property, you’ll be equipped with a valuable tool for solving problems both in the classroom and in everyday life.